
Проблемы Эволюции |
Paleonotological Journal, Vol. 37, No. 2, 2003, P. 107-115.
Paleonotological Journal, Vol. 37, No. 2, 2003, P. 107-115.
A. V. Markov
Paleontological Institute of the Russian Academy of Sciences, Profsoyuznaya ul.
123, Moscow, 117997 Russia
e-mail: markov_a@inbox.ru
Abstract---The ratios of coexisting marine phyla (p), classes (c), orders (o), families (f), and genera (g) through the Phanerozoic can be described as an exponential trend. The number of genera can be calculated as an interval between f x (k -- σ) and f x (k + σ), where k is the arithmetic mean of f/o, o/c, and c/p; and σ is their standard deviation. A reconstruction of species diversity by the same method shows a good fit with other independent estimates. A possibility of quantitative approximation of completeness of the fossil record based on the ratios of taxa of different rank is demonstrated.
Key words: Phanerozoic, marine species diversity, completeness of fossil record, biota, evolution.
Received December 18, 2000
The existing paleontological databases enable an analysis of the diversity dynamics of the Phanerozoic marine biota (PMB) at the generic, family, and higher levels. There is no complete species-level database at present, and it is hardly possible to expect its appearance in the near future. This is a consequence of a huge number (hundreds of thousands) of described fossil marine species and the low reliability of the paleontological data at the species level. To understand the general principles of evolution it is, however, necessary to know how the species-level diversity changed during the Phanerozoic. With the lack of direct data, one has to use reconstructions and extrapolations. Several reconstructions of the species diversity dynamics of the PMB have been proposed. One of them is based on a selective calculation of species, based on data of the Zoological Record (Raup, 1976a). Another approach analyzed the dynamics of species abundance of benthic communities (Bambach, 1977; Seilacher, 1977). There is also a method based on a combination of empirical data and theoretical models (Valentine, 1970, 1973; Raup, 1972, 1976b; Raup et al., 1973; Gould et al., 1977; Signer, 1982, 1985; Sepkoski, 1994; see also reviews in Sepkoski et al., 1981; Alekseev, 1998; Benton, 1999). These reconstructions notably differ from each other. Thus, according to one model, the present species diversity is an order of magnitude higher than the Paleozoic level (Valentine, 1970); according to another, it is 4--10 times as high (Signer, 1982, 1985). The third model reconstructs a threefold increase (Raup, 1976a); the fourth, a twofold rise (Bambach, 1977); the fifth shows no increase at all (Raup, 1972, 1976b, Gould et al., 1977). Sepkoski (1994) summed up this amusing discussion. After scrupulous calculations, he concluded that we do not know how much the Cenozoic species diversity increased compared to the Paleozoic one, ranging in guesses from order of magnitude to insignificant values. To date, no serious mathematically assisted attempts to reconstruct the dynamics of species diversity on the basis of the taxa above species level have been proposed. The purpose of the present study is to assess the possibility of restoring the number of lower-rank taxa based on the number of synchronous higher-rank taxa. To achieve this aim one should review time related changes in the number of phyla, classes, orders, families, and genera and reveal patterns in quantitative ratios of taxa of different rank. The data on genera are taken from the database of Sepkoski (1995), data on families, orders, classes, and phyla are from the published review (Sepkoski, 1992). The stratigraphic distribution of taxa is ranged within a Phanerozoic scale divided into 167 intervals that mostly correspond to substages.
Figure 1a illustrates the dynamics of PMB diversity at five taxonomic levels (from genus to phylum). The logarithmic scale of the ordinate axis allows a pictorial comparison of time related changes of variables, which mean values differ by several orders of magnitude.
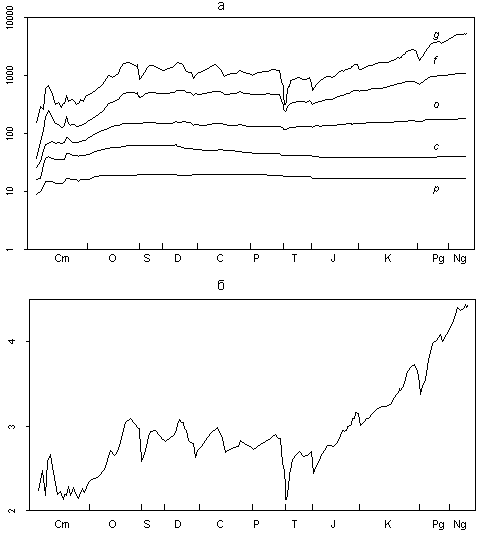
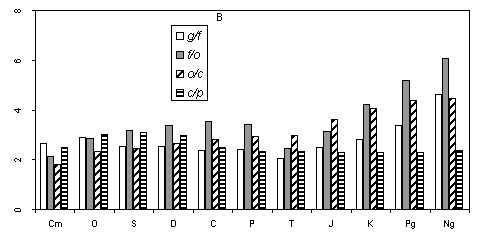
Fig. 1. Relations of the taxa of different ranks in the Phanerozoic marine biota: (a) dynamics of the number of genera (g), families (f), orders (o), classes (c), and phyla (p); (b, c) ordinate axis is logarithmic: (b) coefficient of taxonomic saturation, arithmetical mean of g/f, f/o, o/c, and c/p; and (c) ratios of g/f, f/o, o/c, and c/p, averaged through each period.
The diagram is quite remarkable. The almost parallel course of all five curves throughout the Phanerozoic is striking. In the diagram with a logarithmic scale of the ordinate axis, the vertical distance between any two points shows how much one value is more than the other. The parallelism of curves in Fig. 1a means that at any instant of time an average number of genera in a family did not strongly differ from an average number of families in an order, and likewise orders in a class, and classes in a phylum. Stated another way, the number of taxa of five different ranks (from phylum to genus) at each substage is described by an exponential trend. Although the reasons for this pattern are not quite clear, the stability of numerical ratios of taxa of different ranks during the Phanerozoic is very interesting. The revealed pattern allows as to propose the following equation as a basic model for the description of numerical ratios of taxa of different ranks (in a given substage):
Ni= k·Ni+1, (1)
where Ni is the number of taxa of the ith rank; Ni+1 is the number of taxa of the (I + 1) rank; k is a parameter of the geometrical progression that can vary with time. Changes of the parameter k correspond to fluctuations of the average distance between the curves in Fig.1a. For example, in the Cambrian, the curves are obviously closer to each other than at the end of the Ordovician; a gradual divergence of the curves is noticeable during the Meso-Cenozoic. Based on the logic of the proposed model, the value of k is calculated for each substage according to the formula:
k= (g/f+f/o+o/c+c/p)/4, (2)
where g, f, o, c, and p are the numbers of genera, families, orders, classes, and phyla in the given substage. The parameter k is the average number of taxa of the junior rank in a taxon of the senior rank.
It is worth noting that the proposed model is not final. It is ratherprovisional, tentative, and requires refinement. It could be taken for the final model if all four distances between the curves in Fig. 1a were strictly equidistant, or if deviations from this rule represented minor random noise. However, the observed deviations are not quite random. It is clear that, during large extinctions, the upper curves in the diagram approach each other to a greater extent than do the lower ones. This is particularly evident during the largest extinction at the boundary of the Permian and Triassic. Furthermore, during a large diversification, the upper curves regularly deviated faster than the lowers. These two cases of deviations from the basic model indicate that both extinctions and diversifications affect the lower taxonomic levels much more than the upper ones. This is quiet natural and well known.
With an exponential trend as the basic model for the ratios of the numbers of simultaneously existing taxa of different rank, it is necessary to investigate the variation of k throughout the Phanerozoic. The value of this parameter for each substage was calculated according to formula (2).
The dynamics of k in the Phanerozoic is shown in Fig. 1b. Fluctuations of this parameter are relatively low, ranging from 2.13 at the beginning of the Triassic to 4.2 in the Neogene. In general, the curve resembles the changes of the number of families and genera with one exception in the Cambrian interval. This is not surprising, since the number of lower-rank taxa is subject to considerably higher fluctuations in comparison with higher-rank taxa. Therefore, it is the lower-rank taxa that determine the fluctuations of the averaged k. For the most part, the value of k increased in the Phanerozoic.
To estimate the accuracy of the basic model, it is necessary to consider in more detail the numerical ratios of genera, families, orders, classes, and phyla at different time intervals of the Phanerozoic. As already noted, the proposed model is not ideal. In reality the average number of genera in a family at each particular moment is not equal to the number of families in an order. The same can be stated concerning orders in a class, etc. Factual data shown in Fig. 1a indicate only the same magnitude of these variables. Figure. 1c illustrates the averaged values of g/f, f/o, o/c and c/p for all Phanerozoic periods. It is evident that the four variables somewhat differ depending on the period. Their variation shows certain trends. For example, during the Meso-Cenozoic, the ratio f/o shows a steady growth compared to three other variables. No logical explanation of this picture is currently
available. The diagram in Fig. 1c does not give any clues to the general pattern of interrelations of the four variables (g/f, f/o, o/c, and c/p) within each period. Thus, even with the known values of f/o, o/c, and c/p for a certain time, it is unpredictable whether the values of g/f are more or less than those of f/o. It is naturally not possible to predict if the average number of species in a genus is more or less than g/f. The substage based consideration of the studied variables does not elucidate the situation either.
Nevertheless, Fig. 1c suggests that, given the values of three of the four ratios for a certain time point, it is possible, with some confidence, to predict a range of values containing the fourth (unknown) ratio. It can be shown that it disagrees with the arithmetic mean of the three known ratios by no more than a certain value. For example, through the majority of substages of the Phanerozoic, g/f fits the arithmetic mean of f/o, o/c, and c/p accurate to plus or minus one standard deviation.
With these facts established, we turn to the testing of the model.
The following experiment is necessary to estimate the prognostic value of the model proposed. Let us imagine that there are no data on the stratigraphic distribution of genera, while the data on families, orders, classes, and phyla are available. Let us try to reconstruct the number of described genera in each substage. The solution is based on the model proposed above and variation ranges of variables f/o, o/c, and c/p.
The above statements infer that to determine g on the basis of f, o, c, and p, one should first calculate k for each substage according to the formula:
k = (f/o+o/c+c/p)/3 (3)
<![if !vml]><![endif]>
<![if !mso]><![endif]>
A possible deviation of the average number of genera in a family from k is estimated through the standard deviation calculated for each substage as follows::
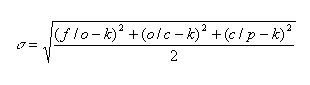
At the next step, we can estimate the interval containing the target value g:
f·(k + s) ? g ? f·(k - s)
The results are displayed in Fig. 2a. Thin lines delimit the calculated range, the thick line shows the empirical number of genera, i.e., the number observed in the fossil record. As clear from the figure, the agreement of the data is striking. Not only is the order of the variable in question predicted correctly, its general dynamics pattern, including ups and downs, is reconstructed with
reasonable accuracy. Recall that the theoretical number of genera was calculated merely based on the number of families and higher taxa, while the data on genera were not used at all.

Fig. 2. Reconstruction of generic diversity based on the taxa above species level (thin curves) and empirically observed number of genera (thick curve), ordinate is logarithmic: (a) basic model, gmin = f x (k -- σ) and gmax = f x (k + σ); and (b) refined model, values of gmin reduced for the periods of large extinctions, gmax increased for the time of the great Ordovician adaptive radiation; ordinate is logarithmic.
The obtained result seems to be very important. It shows a practical opportunity of reasonably precise deduction of lower taxa diversity structure from the data of the upper taxonomic levels only.
Thereby, the model closely fits the empirical data. The next step of the study is the detailed analysis of the observed discrepancies. This procedure would provide our model with the necessary corrections, thus increasing its prognostic
significance.
Let us consider in more detail the relation of empirical data (i.e., actually observed in the record) to the calculated values. For brevity, the empirical number of genera is denoted ge, and the upper and lower boundaries
of the calculated range as gmax and gmin, respectively.
During most of the Phanerozoic, ge does not go beyond the theoretical range (gmax ? ge ? gmin).
The values of ge exceed the upper theoretical limit at the beginning of the Cambrian (Tommotian) and Ordovician (Tremadocian to Arenigian). Both time points coincide with the most intense diversification, the Early Cambrian and Ordovician adaptive radiations. There are six cases where ge went beyond the lower theoretical limit: (1) the time interval close to the
mass extinction at the boundary of the Ordovician and Silurian (Upper Ashgillian to Llandoverian); (2) a series of large extinctions at the boundaries between the Eifelian and Givetian, Frasnian and Famennian, and the Devonian and Carboniferous (the Lower Givetian and the Lower Tournaisian); (3) extinctions at the Serpukhovian-Bashkirian and Carboniferous--Permian boundaries (Serpukhovian to Asselian); (4) the greatest extinction at the boundary of the Permian and Triassic (Dzhulfian to Lower Ladinian); (5) a mass extinction at the boundary of the Triassic and Jurassic (Hettangian to Sinemurian); and (6) extinctions at the boundary of the Jurassic and Cretaceous (Berriasian). During a great extinction at the boundary of the Cretaceous and Paleogene, ge does not leave the theoretical range; however, it comes close to its lower limit. Thus, the clear trend drawn from the diagram of Fig. 1a is evident here. It implies that both great extinctions and diversifications affect the lower taxonomic levels much more than the upper ones. Therefore, the predictions of the number of genera based on the taxa above generic level can lead to underestimated values of the diversity dips during great extinctions and its rises in periods of fast diversification.
With this reasoning in mind, the algorithm of calculation of gmin and gmax is corrected. During large extinctions, gmin should be decreased, whereas the periods of intense diversifications should have increased values of gmax. The required refinements of the model are introduced in the following way. The value of gmin for periods of mass extinctions (boundaries of the Ordovician and
Silurian, the Permian and Triassic, and the second half of the Devonian) should be calculated according to the formula
gmin = f x (k -- 3σ);
for the periods of other large extinctions (Serpukhovian--Bashkirian, Carboniferous--Permian, Triassic--Jurassic, and Creataceous-Paleogene boundaries), the formula is gmin = f x (k -- 2σ). This is quite sufficient to keep ge always above the lower theoretical limit. For the period at the onset of the Ordovician adaptive radiation (Franconian-Arenigian), sufficient correction is expressed by the formula gmin = f x (k +2σ).
The only case where such a light modification does not work is the Tommotian Age. Here, the upper boundary should have been increased according to the formula gmin = f x (k + 20σ). However, this makes the model meaningless. Therefore, we are forced to admit that our model does not fit the factual data on the Tommotian. It is possibly a consequence of a rather poor
data set of this stage in our database. The application of the refined model is shown in Fig. 2b. In this case, the
empirical value of ge is uniformly inside the theoretical range (except for Tommotian Time).
The conducted research shows the possibility of using the data on diversity dynamics at upper taxonomic levels for relatively precise estimates of time-related quantitative changes in described (valid) lower-rank taxa. The technique, which allows for accurate estimations of the number of genera based on the data on families, orders, etc. allows us to infer the number of species
in a similar fashion. To reconstruct the dynamics of species diversity of the PMB (i.e., the number of valid species), k and σ were calculated in the same way as in the case with the number of genera. The only difference is that the empirical data on genera were also included. In each substage, these variables were calculated according to the following formulas:
k = (g/f +f/o+o/c+c/p)/4;
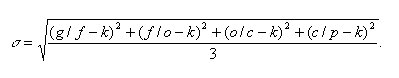
The confidential intervals were determined based on the refined model. For the periods of the largest extinctions, the lower limit of smin was calculated as g x (k -- 3σ); for less significant extinctions, as g x (k --2σ). The upper limit, smax, for the period of the Ordovician diversification was estimated as g x (k + 2σ). For all other substages, the formulas smin = g x (k -- σ) and smin = g x (k + σ) were applied.
The result of this extrapolation is shown in Fig. 3a. The two upper thin curves outline the expected range of s, i.e., the number of species in every substage of the Phanerozoic
.
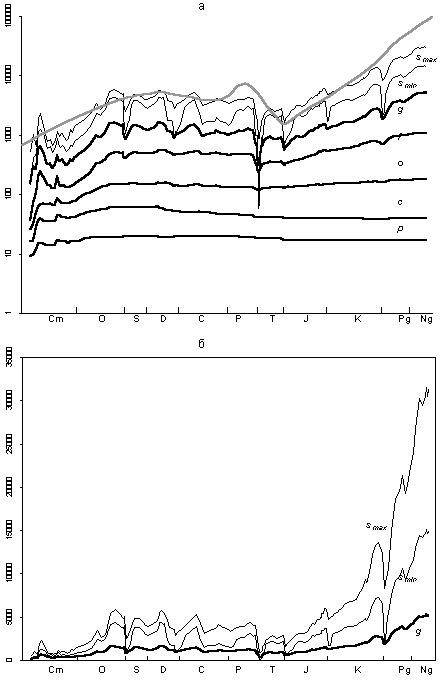
Fig. 3. Reconstruction of species diversity (thin curves), actually observed number of taxa above species level, and empirical model after Valentine (1970, 1973), thick gray curve: (a) ordinate is logarithmic and (b) ordinate is linear.
It is clear that we are dealing not with the species represented in the fossil record rather than with the actual number of species. Possibly, the number of valid species is lower than predicted, because species, in contrast to genera, are poorly understood and their systematics is developed to a lesser extent.
Scientific progress tends to decrease contrasts in the quality of systematics at different taxonomic levels. Therefore, with future improvements in the systematics of marine animals, the actual species number will probably approach the predicted range.
Apart from the problems of taxonomic distinctions, there are other sources of possible errors. Thus, it is evident that the completeness of the fossil record decreases with the lowering of the taxonomic rank. Our estimate of the species number can be overestimated if the incompleteness of the fossil record at the species level is disproportionally higher than that at the generic level.
However, we should take into account the incompleteness of the fossil record at the generic level compared to that at the family level. Nevertheless, this did not prevent us from correct prediction of the numerical dynamics of the genera based on the data on families and higher taxa. Therefore, there are grounds to hope that our deduction of the species number from the data on supraspecific taxa is reasonably accurate as well. The question of the incompleteness of the fossil record is considered in more detail below.
It should be stressed that the reconstruction of the species abundance is based on much more extensive material than in the case of genus-level analysis. Calculations of k and σ for each substage include four instead of three empirical ratios. The addition of g/f to c/p, o/c, and p/o makes the results more confident. The factors distorting the apparent species number should manifest themselves at the generic level at least in the form of incipient trends. These factors are the incompleteness of the fossil record at
low taxonomic levels, growing incompleteness down the stratigraphic scale, the pull of the recent effect, etc. Since the estimates of smin and smax are based on g, and the latter variable is also used in calculations of k and g, all results are affected by these trends.
Thereby, there are reasons to expect a decent accuracy in our reconstruction of the PMB species diversity.
According to our reconstruction (Figs. 3a, 3b), species diversity of the marine biota was rather low in the Cambrian, considerably increased during the Ordovician adaptive radiation, remained stable with incidental fluctuations from the end of the Ordovician to the beginning of the Cretaceous, and sharply increased in the Cretaceous and Cenozoic. The present level of species diversity is 5 or 6 times as highas that in the Paleozoic. In general, our reconstruction is similar to the models of some other authors (Valentine, 1970; Signor, 1982; Sepkoski et al., 1981); however, it is more detailed. Noteworthy is the close correlation of our results with the data on the dynamics of alpha diversity, i.e., species abundance, in benthic communities in the Phanerozoic (Bambach, 1977, Sepkoski, 1988). The alpha diversity was minimal in the Cambrian, sharply increased in the Ordovician, remained almost constant up to the Cretaceous, and again showed a sharp growth in the Cenozoic.
Of the previously published estimates of species diversity of PMB, our reconstruction particularly well fits the "empirical model" proposed by Valentine (1970). This is rather surprising because 30 years ago, available data on the taxonomic diversity of the PMB covered only some groups and were restricted to the family-level only. The number of genera stayed in the area of guesses. With no complex mathematical methods applied, Valentine, nevertheless, could draw a curve of dynamics of the PMB species diversity, which is very similar to the reconstruction proposed here (Fig. 3a). The single important distinction of the Valentine's model is the sharper growth of species diversity in the Cretaceous and Cenozoic. This stems from the method used. Valentine calculated s for the Recent Time on the basis of present day diversity rather than the fossil record, as he did for the rest of the curve. According to his estimates, the extant marine biota includes about 100 000 potentially well fossilized species. It is this value that appeared in his graph. However, the incompleteness of the fossil record was not taken into account. It is evident that not all potentially well fossilized species have the chance to be detected in the fossil record. Other points in the Valentine's curve are calculated or, more precisely, approximated on the basis of the fossil data.
The results of our study allow for comments on possible distortions and constant bias to be accounted for by the differential incompleteness of the fossil record.
Increased Incompleteness at Low Taxonomic Levels It is evident and needs no proofs that the incompleteness increases with the lowering of taxonomic rank. It is clear that, of the total number of the potentially well fossilized taxa of the past, the proportion of genera known to paleontologists is much lower than that of families. However, it is not known how much this influences the picture of dynamics of the PMB taxonomic diversity. As was demonstrated, the proportion of simultaneously existing taxa of different
ranks in the Phanerozoic is well described by an exponential trend. The same regular trend is also known for the extant biota. If the percent of fossilized genera were much lower than that of families, this would be seen in the proportions of taxa of different ranks in the fossil record. Assume that, in the real biota from each substage, the average number of genera in a family was approximately equal to the average number of families in an order, and the orders are completely presented in the fossil record. Let us designate the probability of preservation (or, more precisely, the presence of a published description) of a family and a genus in a substage as rf and rg, respectively. Hence, the numbers of genera and families actually existing in a substage are g/rg and f/rf. Consequently,
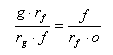
Thus, it is possible to deduce a relationship of preservation probabilities of families and genera as follows:
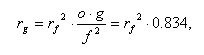
since the mean Phanerozoic value of og/ f2 is known to be 0.834.
This dependence is shown by a curve in Fig. 4a. The shape of the curve indicates that the preservation probability of genera may be much lower than that of families only at very low values for both. Apparently, this is the case in the groups without mineralized skeletons. On the contrary, if the preservation probability of families is high, the preservation of genera should imply a not be much lower.
This inference can be compared with the empirical estimates of Foote and Sepkoski (1999). For the main groups of marine animals, they compared the proportion of extant families registered in the fossil record with the probability of genus preservation calculated according to the method proposed by Foote and Raup (Foote and Raup, 1996; Foote, 1997). The study revealed a high
correlation of the two independent completeness measures. As expected, the probability of genus preservation turned out to be somewhat lower than at the family level. Results of Foote and Sepkoski for various groups of marine animals are shown in Fig. 4a. Evidently, most of the points are plotted not far from our curve of the theoretical relation of preservation probability of families and
genera.
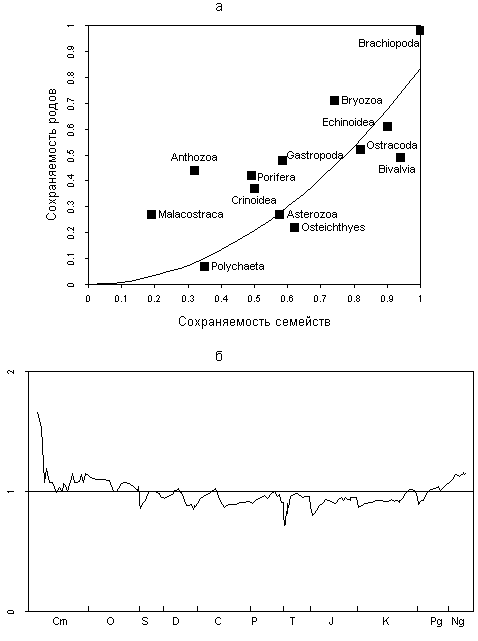
Fig. 4. Influence of the incompleteness of the fossil record on the apparent taxonomic diversity: (a) preservation probability of genera and families in the fossil record (curve), data for various groups (black squares) after Foote and Sepkoski (1999), vertical axis: probability of preservation of genera; horizontal axis: proportion of extant families in fossil record; and (b) relative generic abundance.
The data from Fig. 4a enable a rough estimate of absolute means of rg and rf for fossil marine animals. The average preservation probability of animals with a mineralized skeleton is about 70% for families and 45% for genera (rf » 0.7; rg » 0,45)<![if !supportFootnotes]>[1]<![endif]>).
Pull of the Recent. The other important constant bias of the existing paleontological databases is called the pull of the recent (Raup, 1979). It is based on a better knowledge of the living biota compared to a biota of any instant of the geological past.
Thus, an extant deep-sea genus known in the fossil record by a single Late Cretaceous occurrence would be considered living throughout the Cenozoic. However, if the Recent biota was studied with a precision currently available for the fossil record, we would regard the genus in question as extinct in the Late Cretaceous. Judging by the share of taxa surviving till the Recent, this
effect should be noticeable at the generic and family levels, starting at about the mid-Mesozoic and abruptly increasing toward Recent Time. The effect of the pull of the recent is obviously based on the incompleteness of the fossil record and, consequently, increases in lower-rank taxa. Both effects (a lower completeness at low taxonomic levels and pull of the recent) are thought to be well manifested in Fig. 2a. Let us compare the number of genera inferred from the number of suprageneric taxa (gmin and gmax) with the empirical values of the fossil record (ge). Since both effects should influence the genera to a much greater extent than the families or, more so, orders, they are likely not manifested in the theoretical range, whereas ge should be affected.
From the Silurian up to the Cretaceous, ge is noticably closer to the lower limit of the predicted range, gmin. This bias is presumably a result of the first effect considered above, that is, a dearth of detected genera in comparison with the values expected from the number of suprageneric taxa. This shortage is not seen, except for in the Cambrian and Ordovician, possibly due to an extremely intense diversification. However, in the mid-Cretaceous onward, ge gradually moves from the lower limit of the predicted range to its middle. In the Cenozoic, ge is closer to gmax. This increase in ge is likely a clear effect of the pull of the recent. In the Cretaceous and Cenozoic, the two effects causing biases compensate each other almost completely. As a result, the apparent behavior of ge accurately fits the predictions.
Age Related Increase in Incompleteness. Another constant bias in the PMB fossil record discussed in the literature is associated with the presumed growth of incompleteness of the record down the time scale. Raup (1972, 1976b) was the first who attracted attention of paleontologists to this problem. He assumed that the species diversity could reach the modern level already in the Paleozoic with no appreciable growth since that time. The observed increase in diversity can be an artifact of the growing
informativeness of the fossil record up the stratigraphic scale. Since the works of Raup, the problem of the confidence in the estimates of the fossil diversity has been hotly debated. The majority of paleontologists believe that Raup considerably overestimated this effect. According to their viewpoint, the apparent diversity is close to the actual values (Benton, 1999).
These are the most important arguments against the Raup's model:
(1) An increasing overall diversification of biachores in the Phanerozoic. This should lead to an increase in gamma diversity (diversity of regional faunas) and influence the general diversity of the biota. Hence, it is unlikely that the Paleozoic species diversity matches the Recent level (Valentine, 1973).
(2) The alpha diversity (average species number in marine benthic communities) increased through the Phanerozoic. This variable is not biased by the differential incompleteness of the fossil record. The dynamics of alpha diversity shows a good correlation to empirical estimates of the dynamics of the general species diversity of PMB (Bambach, 1977; Sepkoski, 1988).
(3) Independent databases and different methods applied lead different researches to similar estimates of the dynamics of the PMB diversity, notwithstanding the expected differential influence of the constant biases in the fossil record on these results (Sepkoski et al., 1981).
(4) Mathematical modeling has shown that, even if the main biases pointed out by Raup (differences in volume and exposed area of the deposits of different age and in the number of paleontologists who study faunas of different age) are maximally taken into account, the actual dynamics of the species diversity is still closer to the empirical model of Valentine (1973) than to Raup's model (Signor, 1982).
(5) The comparison of chronological succession of the appearance of taxa in the fossil record with the sequence inferred from the published phylogenetic schemes shows their stable correlation throughout the Phanerozoic. If the informational quality of the fossil record noticeably grew with time, the agreement between the two would also increase (Benton et al., 2000).
The above results allow one to add one more argument to this list. It is evident that the incompleteness of the fossil record should be higher at the generic level than at the family or ordinal levels. Hence, if the incompleteness appreciably grew from the Neogene to Cambrian, this would result in a constant growth of ge relative to gmin and gmax through the Phanerozoic. We,
however, do not observe this, except for the Cretaceous and Cenozoic, which is easier to explain using the pull of the recent using than the changes in the completeness of the fossil record.
There is a general way to check if the number of empirically observed Phanerozoic genera is excessive or deficient against the estimates inferred from the number of suprageneric taxa. For this purpose, the relative generic abundance is calculated as follows:
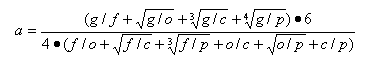
This variable equals one if the empirical number strictly corresponds to the value expected from the ratios of higher taxa; it is more than one if the empirical values are greater than expected; and it is less than one in the case of a deficiency of genera. If the generic completeness of the PMB fossil record considerably decreases down the time scale, the variable should increase during the Phanerozoic. The changes of the relative generic abundance with time are showed in Fig. 4b. As seen in the graph, no general increase is observed. We see the same trends as noted above with ge, gmax, and gmin. The number of genera is overestimated in the Cambrian and Ordovician. It stems from the intense diversification of marine organisms at that time, and also from problems in classification of the oldest forms, with many valid genera still not attributed to higher taxa. The generic abundance is underestimated in the Silurian to the Cretaceous (possibly becaused of a relative incompleteness of the fossil record at the generic level compared to the higher-rank taxa) and overestimated somewhat in the Cenozoic (most likely as a result of the pull of the recent).
The results obtained indicate a relatively low influence of the main constant biases usually expected in the fossil record on the apparent picture of diversity changes. The first bias, increased incompleteness of the fossil record in the lower-rank taxa, is only manifested in a somewhat decreased number of genera, compared to the predicted, from the Silurian to the Cretaceous. The pull of the recent at the generic level is observable in the Cretaceous and Cenozoic. In this period, it acts mostly as a refining agent compensating the effect of the first bias. The age-related growth of incompleteness of the fossil record is not observed at all.
A comparison of direct estimates of the number of extant species, 100 000 (Valentine, 1970, 1973), and the values obtained by our reconstruction, 15000-30000, gives a rough idea of the completeness of the fossil record at species level for well fossilized groups. Each interval (substage) of the studied part of the fossil record apparently shows 15--30% of potentially well fossilized species existed at that time. Here, an interval is characterized by both the species discovered within its span and known from under- and overlying deposits. This is in a good agreement with the above cited data on the preservation probability of genera (45%) and families (70%) in well fossilized groups.
All these things suggest that the fossil record of the PMB is actually more complete than usually thought. In particular, all calculations and conclusions of the present study will stay valid if the empirical values of g and f are substituted by the number of actually existing genera and families derived the from data of Foote and Sepkoski. To do this, g and f in each substage should
be divided by 0.45 and 0.75, respectively. Results of this experiment are the following:
(1) The two upper curves in Fig. 1a rise slightly, not disturbing the general parallel course of curves. The data still remain in good agreement with the basic model that implies the ratios of taxa of different rank in any substage are described by an exponential function.
(2) The number of genera reconstructed on the basis of the number of suprageneric taxa (see Fig. 2a) appears more accurate. The variable ge does not cross the lower theoretical limit, gmin, and is generally closer to gmax. As before, ge exceeds the upper theoretical limit in the Cambrian and the beginning of the Ordovician, as well as in the middle of the Triassic during
the intense diversification that followed the great extinction in the terminal Permian. Therefore, there is no need to lower the gmin during periods of mass extinctions (Fig. 2b).
(3) The number of species deduced from the number of taxa above species level turn out to be on the average 2.5 times higher than is shown in Fig. 3, with the upper limit of smax being 3.3 times higher than the middle of the range in Fig. 3. These results completely fit the above noted estimate of the species-level completeness of the fossil record: every substage retains up to
30% of species, i.e., there were 3.3 times more species than those preserved. In this context, the left part of the Valentine's curve (the Paleozoic and Mesozoic) appears much below the predicted lower limit smin, whereas its right, Cenozoic, part remains entirely within the limits of the predicted range of s. The modern level of species diversity this time accurately coincides with the estimate obtained by Valentine (about 100 000). It means that our calculations are quite sound.
(1) In the Phanerozoic marine biota, the numerical ratios of simultaneously existing taxa of different ranks (from phylum to genus) is well described by an exponential trend. The ratios g/f, f/o, o/c, and c/p in each substage are of the same order. In the majority of substages of the Phanerozoic, each variable is within the limits of the arithmetic mean of the three others with the accuracy of plus or minus σ.
(2) By the number of phyla, classes, orders, and families existing at a certain time point, it is possible with a reasonable accuracy to reconstruct the number of genera as the values ranging from f x (k -- σ) to f x (k + σ), where k is the arithmetic mean of f/o, o/c, and c/p and σ is their standard deviation. The same method allows one to estimate the number of species on the basis of the taxa above species level.
(3) The reconstructed dynamics of the PMB species diversity is in good agreement with other independent estimates. Species diversity of the marine biota was minimal in the Cambrian, sharply increased in the Ordovician, remained approximately constant up to the Cretaceous, and showed a sharp growth in the Cenozoic. The modern level is 5 or 6 times as high as in the Paleozoic.
(4) The study of the ratios of taxa of different ranks in different geological epochs allows one to estimate the influence of differential incompleteness of the fossil record on the observed dynamics of the PMB diversity. The incompleteness of the fossil record likely distorts the actual picture but slightly and in a quit predictable way. An increase in incompleteness at the lower taxonomic levels manifests itself in the minor deficiency of lower-rank taxa compared to expected values. The effect of the pull of the recent is noticeable at the generic level since the Cretaceous. It acts as a refining agent compensating the effect of the first bias. The hypothetical decrease in the informational value of the fossil record down the time scale is not observed.
(5) The studied portion of the fossil record of organisms with mineralized skeletons apparently comprises about 15--30% of species, 45% of genera, and 70% of families actually existing in the past. The introduction of corrections intended to reconstruct the actual number of taxa does not falsify the obtained results but makes them more reliable.
ACKNOWLEDGMENTS
This study was supported by the Russian Foundation for Basic Research, project no. 00-05-65020.
Alekseev, A.S., Mass Extinctions in the Phanerozoic, Doctoral (Geol.-Mineral.) Dissertation, Moscow: Moscow State University, 1998.
Bambach R.K. Species richness in marine benthic habitats through the Phanerozoic // Paleobiology. 1977. V. 3. № 2. P. 152-167.
Benton M.J. The history of life: large databases in palaeontology // Numerical Palaeobiology. Computer-based modelling and analysis of fossils and their distributions. Chichester – N. Y. etc.: Wiley and Sons, 1999. P. 249-283.
Benton M.J., Wills M.A., Hitchin R. Quality of the fossil record through time// Nature. 2000. V. 403. № 6769. P. 534-537.
Foote M. Estimating taxonomic durations and preservation probability // Paleobiology. 1997. V. 23. P. 278-300.
Foote M., Raup D.M. Fossil preservation and the stratigraphic ranges of taxa // Paleobiology. 1996. V.22. № 2. P. 121-140.
Foote M., Sepkoski J.J. Absolute measures of the completeness of the fossil record // Nature. 1999. V. 398. № 6726. P. 415-417.
Gould S.J., Raup D.M., Sepkoski J.J., Schopf T.J.M., Simberloff D.S. The shape of evolution: A comparison of real and random clades // Paleobiology. 1977. V. 3. P. 23-40.
Raup D.M. Taxonomic diversity during the Phanerozoic // Science. 1972. V. 177. P. 1065-1071.
Raup D.M. Species diversity in the Phanerozoic: a tabulation // Paleobiology. 1976а. V. 2. № 4. P. 279-288.
Raup D.M. Species diversity in the Phanerozoic: an interpretation // Paleobiology. 1976б. V. 2. № 4. P. 289-297.
Raup D.M. Biases in the fossil record of species and genera // Bull. Carnegie Museum Natur. History. 1979. №13. P. 85-91.
Raup D.M., Gould S.J., Schopf T.J.M., Simberloff D. Stochastic models of phylogeny and the evolution of diversity // J. Geol. 1973. V. 81. № 5. P. 525-542.
Seilacher A. Evolution of trace fossil communities // Patterns of evolution as illustrated by the fossil record. Amsterdam: Elsevier, 1977. P. 359-376.
Sepkoski J.J. Alpha, beta or gamma: where does all the diversity go? // Paleobiology. 1988. V. 14. № 3. P. 221-234.
Sepkoski J.J. A compendium of fossil marine animal families. 2nd edition // Milwaukee Public Museum Contr. Biol. and Geol. 1992. № 83. 156 p.
Sepkoski J.J. Limits to randomness in paleobiologic models: the case of Phanerozoic species diversity // Acta palaeontol. polon. 1994. V. 38. № 3-4. P. 175-198.
Sepkoski J.J., Bambach R.K., Raup D.M., Valentine J.W. Phanerozoic marine diversity and the fossil record // Nature. 1981. V. 293. № 5832. P. 435-437.
Signor P.W. Species richness in the Phanerozic: compensating for sampling bias // Geology. 1982. V. 10. № 12. P. 625-628.
Signor P.W. Real and apparent trends in species richness through time // Phanerozoic diversity patterns: Profiles in Macroevolution. Princeton: Princeton Univ. Press, 1985. P. 129-150.
Valentine J.W. How many marine invertebrate species? A new approximation // J. Paleontol. 1970. V. 44. № 3. P. 410-415.
Valentine J.W. Phanerozoic Taxonomic Diversity: A Test of Alternate Models // Science. 1973. V.180. № 4090. P. 1078-1079.